Subequivariant Meshgraphnets
Luna Fredenslund, Peter J Adema, Patrick Jensen.
Learning physical simulators has become a topic of some focus within deep learning, with many current approaches being based on Graph Neural Networks (GNNs). Two papers on this topic are Pfaff et al., proposing MeshGraphNets (MGNs), models capable of accurately replicating mesh-based simulations, and Han et al., proposing a learned rigid-body simulator augmented with the physical prior of rotational subequivariance. We propose two augmentations of MGN using the subequivariant transform from Han et al. Training and evaluating the modified models at a smaller scale shows that wrapping every non-linear element with a subequivariance transform can enable both accurate predictions and generalization under rotation while increasing data efficiency, at the cost of computational efficiency. Our results show a promising direction for future research on models of larger scales, serving as a compelling proof of concept for subequivariant mesh simulation using GNNs.
PDF, Github
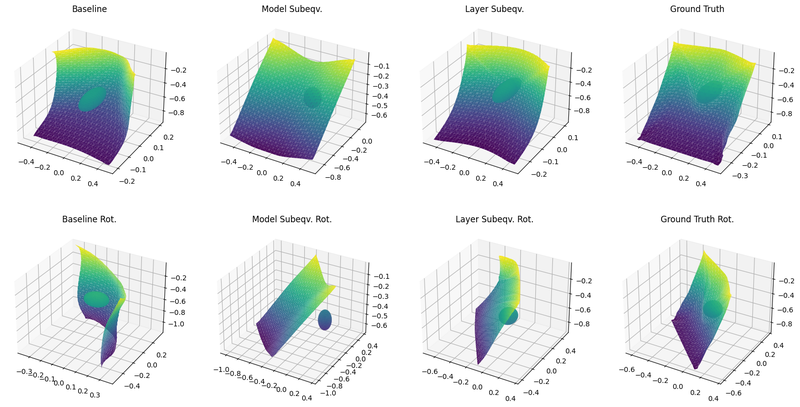
Figure 1: A qualitative look at how the different models perform under rotation around a subequivariant axis.
Graph based neural networks are promising for physics simulations due to their flexibility and how they can scale to larger and more complex geometries. However, the key to solving many physics problems is to identify and exploit the symmetries of the problem. Traditional deep learning approaches neglect this instead letting the models implicitly learn the symmetries for example through train time augmentation. We want to encode the symmetry into the model following Han et al. The method is outlined in Figure 2.
This is an experiment trying to extend Learning Mesh-Based Simulation with Graph Networks which remains competitive in mesh based simulation by making the model subequivariant as described in Learning Physical Dynamics with Subequivariant Graph Neural Networks. The experiment was performed as part of the course Advanced Topics in Deep Learning.
Self consistency
Due to the limited compute budget available of $50 USD, we had to drastically scale down the complexity of the models leaving us unable to provide absolute measures of performance to compare.
However, we are able to test how well each model encode the symmetry of our problem by rotating around the subequivariant axis and measuring how inconsistent the predictions are before and after rotation. We define the metric
$$MSE_{eqv} = \frac{1}{N}\sum_i^N \|model(\vec{x^t})-\mathbf{R}^{-1} model(\mathbf{R}\vec{x^t})\|_2^2$$
where $\mathbf{R}\in\mathbb{R}^{3\times 3}$ is some rotation matrix around the subequivariant axis, and $\mathbf{R}^{-1}$ is the inverse of that rotation. $\vec{x}_i\in\mathbb{R}^{3\times \mathcal{N}}$ is the world space coordinates for $\mathcal{N}$ nodes at time $t$.
The results are summarized in Table 1.
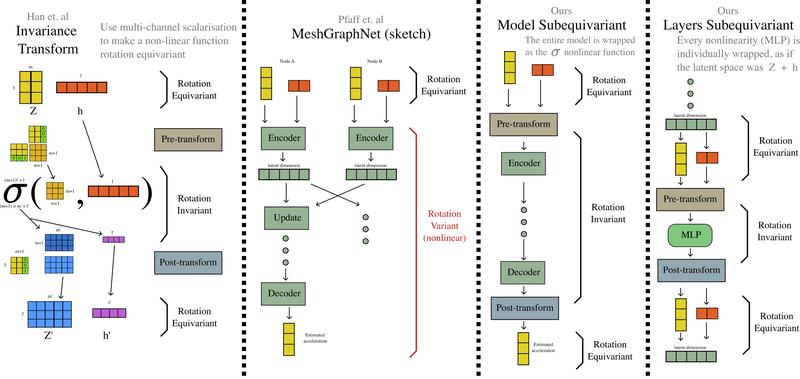
Figure 2: Showcasing the proposed modifications to enable subequivariace.
| $MSE_{subeqv}$ | Machine Precision | Base | Model Subeqv. | Layer Subeqv. |
|---|---|---|---|---|
| Step 5 | $(2.6\pm 0.7)\cdot 10^{-16}$ | $(3\pm 1)\cdot 10^{-5}$ | $(8\pm 2)\cdot 10^{-15}$ | $(2.3\pm 0.9)\cdot 10^{-6}$ |
| Step 500 | $(2\pm 1)\cdot 10^{-16}$ | $(3\pm 2)\cdot 10^{-2}$ | $(3\pm 6)\cdot 10^{-5}$ | $(10\pm 3)\cdot 10^{-4}$ |
We see that both the extensions made to Pfaff et al. improve the self-consistency under equivariant transformation. The model-wise extension is close to the machine precision of just the transformation, but the error propagates faster through the timesteps due to the extra computations involved in unrolling the simulation. The layer-wise is somewhat less equivariant compared to the model-wise, but achieves a better $MSE_{abs}$ of $0.2\pm 0.3)\cdot 10^{-5}$ at step 5 compared to $(0.4\pm 0.2)\cdot 10^{-5}$ for the base model and an even greater difference to the model-wise extension which performs slightly worse compared to the baseline. The rankings hold at step 500 as well.
We see that the ability of the layer-wise subequivariant model to observe only relative angles allows for better accuracy, generalization and data efficiency (using only 40% of the training epochs as the other models) at the price of being six times slower.
For the full discussion and details regarding the implementation, you can read the full paper.
