Grid search is a common method of hyper parameter optimization. Since we cannot get the gradients of hyper parameters, a seemingly good method is to systematically try all combinations of parameters.

However, there is a better method. Usually all variables in a problem are not equally important. Some parameters dominate the performance while some might little if at all. But you don't know which variables are the important variables, so what do we do?

Instead of using grid search, we can use random search. The idea being that in a grid search paradigm, we reevaluate the same value for each variable many times, whereas in a random search setting, we evaluate new values of each variable each time.

So if we have two variables, one important one, and one unimportant one, in grid search, we only get a fraction as many evaluations for the important variable compared to the random search one. We can see this illustrated on the image below.

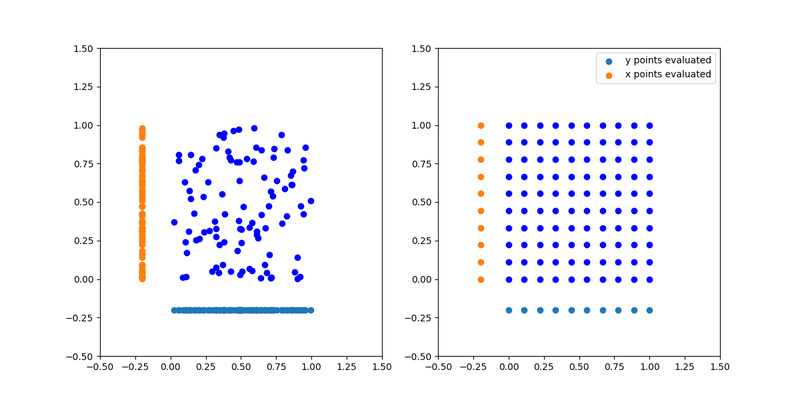
We see that for the important 'x' variable, we get 100 different evaluations in the random search scheme whereas we only get 10 evaluations for the important variable in the grid search scheme.