There are many resources for implementing Dijkstra's algorithm for graphs on the internet, but there are few resources for implementing the algorithm for the special case where the graph is a 2d grid with obstacles. Moreover, the various library implementations all assume some sort of graph data structure which makes sense; graphs are the natural structure for the algorithm, and you could convert an obstacle-grid to a graph. However, sometimes all you want and need is a 2d grid which is exactly what I have implemented for your convenience. If you just want the code, you can find it at the end of the article, but first let us discuss the algorithm.
Dijkstra's Algorithm
Dijkstra's algorithm is an algorithm for finding the shortest path between two points potentially avoiding obstacles on the way. It works by exploring the distances to all nodes in the grid starting at the source node, always considering the shortest path yet, until the desired node is found in a bread-first search manner.
The idea is to choose a tile that is the current shortest path, and then compute the distance to neighbouring tiles (up down left right) repeat until the destination node is found.
- Initialize the distances as "infinite" and mark all tiles in the matrix as unvisited. Furthermore, initialize an obstacle matrix that contains ones for all tiles except the obstacles which contain a very high number - "infinite", so we discourage the algorithm from going to those tiles.
- Set the distance of the entry and destination tile to 0, indicating that it can be reached directly from the source.
- Repeat the following steps until all vertices have been visited:
- Select the unvisited tile with the smallest distance from the source.
- Mark this tile as visited.
- For each unvisited neighbor (up down left right) of this tile, calculate the distance to that neighbor as the sum of the distance to the current tile and the cost of moving on that tile. If this distance is smaller than the current estimated distance to the neighbor, update the neighbor's distance with the new value - Once we have reached the destination tile, the algorithm is finished, and we have found the shortest path.
In code, we get:
Initialize the maps:
# initialize cost heuristic map
obstacles = obstacles.copy()
# obstacles should have very high cost, so we avoid them.
obstacles *= 1000
# normal tiles should have 1 cost (1 so we can backtrack)
obstacles += np.ones(obstacles.shape)
# source and destination are free
obstacles[initial_node[0],initial_node[1]] = 0
obstacles[desired_node[0],desired_node[1]] = 0
# initialize maps for distances and visited nodes
size_of_floor = obstacles.shape[0]
# we only want to visit nodes once
visited = np.zeros([size_of_floor,size_of_floor],bool)
# initiate matrix to keep track of distance to source node
# initial distance to nodes is infinity so we always get a lower actual distance
distances = np.ones([size_of_floor,size_of_floor]) * np.inf
# initial node has a distance of 0 to itself
distances[initial_node[0],initial_node[1]] = 0Then we repeat the following:
For each potential direction we can go (up down left right), we check that the potential tile is valid (within the grid) and not visited.
directions = [up, down, left, right]
for direction in directions:
potential_node = direction(current_node)
if valid_node(potential_node, size_of_floor): # boundary checking
if not visited[potential_node[0],potential_node[1]]:If so, we want to update the distance to that node if it's the shortest path to that node we have discovered so far.
# update distance if it is the shortest discovered
if distance < distances[potential_node[0],potential_node[1]]:
distances[potential_node[0],potential_node[1]] = distanceFinally, after exhausting all the potential nodes, we mark the current node as visited, and choose the next node to be the node with the current shortest path.
# mark current node as visited
visited[current_node[0] ,current_node[1]] = True
# select next node
# by choosing the the shortest path so far
t=distances.copy()
# we don't want to visit nodes that have already been visited
t[np.where(visited)]=np.inf
# choose the shortest path
node_index = np.argmin(t)
# convert index to row,col.
node_row = node_index//size_of_floor
node_col = node_index%size_of_floor
# update current node.
current_node = (node_row, node_col)If the next node we select is the destination node, we stop the algorithm, and backtrack to get the actual path.
Backtracking is very simple, we just start with the destination node, and choose the next node to be the one with the shortest distance in a greedy fashion until we reach the source node.
The code
(for copy-pasting)
import numpy as np
def valid_node(node, size_of_grid):
"""Checks if node is within the grid boundaries."""
if node[0] < 0 or node[0] >= size_of_grid:
return False
if node[1] < 0 or node[1] >= size_of_grid:
return False
return True
def up(node):
return (node[0]-1,node[1])
def down(node):
return (node[0]+1,node[1])
def left(node):
return (node[0],node[1]-1)
def right(node):
return (node[0],node[1]+1)
def backtrack(initial_node, desired_node, distances):
# idea start at the last node then choose the least number of steps to go back
# last node
path = [desired_node]
size_of_grid = distances.shape[0]
while True:
# check up down left right - choose the direction that has the least distance
potential_distances = []
potential_nodes = []
directions = [up,down,left,right]
for direction in directions:
node = direction(path[-1])
if valid_node(node, size_of_grid):
potential_nodes.append(node)
potential_distances.append(distances[node[0],node[1]])
least_distance_index = np.argmin(potential_distances)
path.append(potential_nodes[least_distance_index])
if path[-1][0] == initial_node[0] and path[-1][1] == initial_node[1]:
break
return list(reversed(path))
def dijkstra(initial_node, desired_node, obstacles):
"""Dijkstras algorithm for finding the shortest path between two nodes in a graph.
Args:
initial_node (list): [row,col] coordinates of the initial node
desired_node (list): [row,col] coordinates of the desired node
obstacles (array 2d): 2d numpy array that contains any obstacles as 1s and free space as 0s
Returns:
list[list]: list of list of nodes that form the shortest path
"""
# initialize cost heuristic map
obstacles = obstacles.copy()
# obstacles should have very high cost, so we avoid them.
obstacles *= 1000
# normal tiles should have 1 cost (1 so we can backtrack)
obstacles += np.ones(obstacles.shape)
# source and destination are free
obstacles[initial_node[0],initial_node[1]] = 0
obstacles[desired_node[0],desired_node[1]] = 0
# initialize maps for distances and visited nodes
size_of_floor = obstacles.shape[0]
# we only want to visit nodes once
visited = np.zeros([size_of_floor,size_of_floor],bool)
# initiate matrix to keep track of distance to source node
# initial distance to nodes is infinity so we always get a lower actual distance
distances = np.ones([size_of_floor,size_of_floor]) * np.inf
# initial node has a distance of 0 to itself
distances[initial_node[0],initial_node[1]] = 0
# start algorithm
current_node = [initial_node[0], initial_node[1]]
while True:
directions = [up, down, left, right]
for direction in directions:
potential_node = direction(current_node)
if valid_node(potential_node, size_of_floor): # boundary checking
if not visited[potential_node[0],potential_node[1]]: # check if we have visited this node before
# update distance to node
distance = distances[current_node[0], current_node[1]] + obstacles[potential_node[0],potential_node[1]]
# update distance if it is the shortest discovered
if distance < distances[potential_node[0],potential_node[1]]:
distances[potential_node[0],potential_node[1]] = distance
# mark current node as visited
visited[current_node[0] ,current_node[1]] = True
# select next node
# by choosing the the shortest path so far
t=distances.copy()
# we don't want to visit nodes that have already been visited
t[np.where(visited)]=np.inf
# choose the shortest path
node_index = np.argmin(t)
# convert index to row,col.
node_row = node_index//size_of_floor
node_col = node_index%size_of_floor
# update current node.
current_node = (node_row, node_col)
# stop if we have reached the desired node
if current_node[0] == desired_node[0] and current_node[1]==desired_node[1]:
break
# backtrack to construct path
return backtrack(initial_node,desired_node,distances)For running the code:
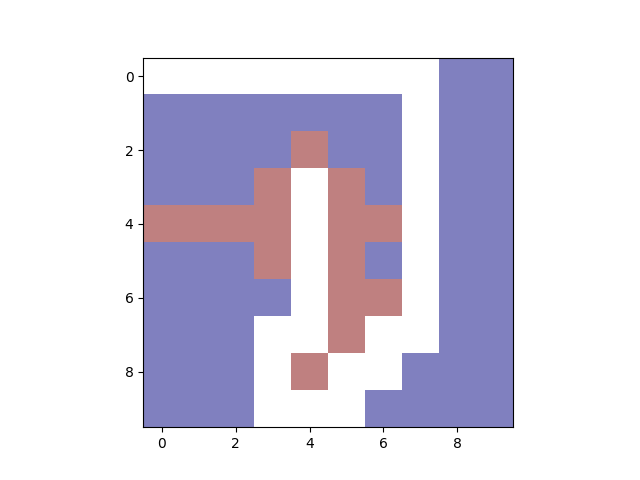
import matplotlib.pyplot as plt
obstacles = np.array([[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0,0,0],
[0,0,0,1,0,1,0,0,0,0],
[1,1,1,1,0,1,1,0,0,0],
[0,0,0,1,0,1,0,0,0,0],
[0,0,0,0,0,1,1,0,0,0],
[0,0,0,0,0,1,0,0,0,0],
[0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0]], dtype=float)
path = dijkstra([0,0],[3,4],obstacles)
print(path)
p = np.zeros(shape=obstacles.shape)
for i in range(len(path)):
p[path[i][0],path[i][1]] = np.nan
plt.imshow(p+obstacles, cmap='jet')
plt.show()